Численный расчёт цифровой голографической интерферометрии на платформе CUDA
Назначение: цифровое голографическое восстановление и цифровая голографическая интерферометрия на платформе CUDA по реальным цифровым голограммам.
Область применения: цифровая голография, цифровая голографическая микроскопия, оптическая физика.
Используемый алгоритм: метод преобразования Френеля, метод фильтрации высоких частот для подавления нулевого порядка дифракции, метод цифровой голографической интерферометрии.
На вход программы подается файл изображения с голограммой, полученной цифровым путем. При помощи выбранного метода по голограмме восстанавливается изображение объекта, который был записан на этой голограмме. В основе методов восстановления лежит численное решение интеграла Френеля-Кирхгофа [1]. В методе преобразования Френеля используется разложение части подынтегрального выражения в ряд Тейлора и приведение интеграла к преобразованию Фурье. Перед голографическим восстановлением осуществляется дополнительная обработка голограммы с целью подавления нулевого порядка дифракции для улучшения качества результата [2]. Для этого используется адаптивный частотный фильтр. Для реализации цифровой голографической интерферометрии используются 2 голограммы. Разница между их численными восстановлениями по фазе позволяет восстановить трёхмерную деформационную модель по всей видимой поверхности измеряемого объекта [3].
- Рябухо, В. П. Когерентно-оптические методы в измерительной технике и биофотонике: Учебное пособие / В. П. Рябухо, В. В. Тучин. – Саратов: Сателлит, 2009. – 127 с.
- Kreis, T. Suppression of the dc term in digital holography / T. Kreis, W. Juptner // Optical Engineering. – 1997. – Vol. 36. – P. 2357-2360.
- Schnars, U. Direct phase determination in hologram interferometry with use of digitally recorded holograms / U. Schnars // JOSA A. – 1994. – Vol. 11(7). – P. 661-665.
Функциональные возможности: цифровое голографическое восстановление реальных голограмм с подавлением нулевого порядка дифракции при различных параметрах восстановления (длина волны, расстояние восстановления, угол отклонения опорного пучка, физический размер пикселя в голограмме и др.).
Программный продукт выполняет следующие функции:
- восстановление цифровой голограммы, используя последовательный алгоритм для CPU (для размера голограмм со сторонами от 256 до 4096 пикселей);
- восстановление цифровой голограммы, используя параллельный алгоритм для GPU CUDA (для размера голограмм со сторонами от 256 до 4096 пикселей);
- осуществление ЦГИ, используя последовательный алгоритм для CPU (для размера голограмм со сторонами от 256 до 4096 пикселей);
- осуществление ЦГИ, используя параллельный алгоритм для GPU CUDA (для размера голограмм со сторонами от 256 до 4096 пикселей).
Инструментальные средства создания: Microsoft Visual Studio 2012, С++, CUDA Toolkit 6.5.
Работа с программой: в приложенном архиве располагается программа для OC Windows в виде исполняемого файла (папка redist) и в виде исходного кода (папка src). Для запуска программы необходимо запустить файл Holo.exe или примеры (run_experiment1.bat и run_experiment2.bat). В папке redist также можно найти подробное руководство по работе с программой (users_manual.pdf).
Общие:
1) OC Windows 7 и выше
2) Оперативная память не менее 2ГБ
Для запуска исполняемого файла:
1) Visual C++ Redistributable for Visual Studio 2012 (http://www.microsoft.com/en-us/download/details.aspx?id=30679)
2) CUDA Toolkit 6.5 (https://developer.nvidia.com/cuda-toolkit-65)
Для компиляции исходного кода:
1) Microsoft Visual Studio 2012
2) CUDA Toolkit 6.5
Использование технологии CUDA для расшифровки интерференционных картин со случайными фазовыми сдвигами
Назначение: Расшифровка интерференционных картин со случайными фазовыми сдвигами.
Область применения: Цифровая интерферометрия, оптическая физика.
Используемый алгоритм: Алгоритм расшифровки интерференционных картин со случайными фазовыми сдвигами [1]
Алгоритмы анализа интерференционной структуры на основе фазовых сдвигов широко используются при создании интерференционных измерительных систем. Точность существующих алгоритмов анализа зависит от точности установки фазовых сдвигов. Однако, на практике сложно определить точное значение фазового сдвига из-за ошибки фазосдвигающего устройства. В программе используется новый алгоритм для расшифровки интерференционных картин. Алгоритм использует три интерференционные картины с произвольными фазовыми сдвигами для нахождения разности фаз между опорным и объектным волновыми фронтами.
Сущность алгоритма заключается в преобразовании траектории интерференционных сигналов (интенсивностей) со случайными фазовыми сдвигами к траектории сигналов, чьи фазовые сдвиги известны точно. Так как в алгоритме отсутствуют итерационные процессы, реализация алгоритма на CUDA отличается своей прямолинейностью и эффективностью.
[1] В.И. Гужов, С.П. Ильиных, Д.С. Хайдуков. Алгоритм расшифровки интерференционных картин со случайными фазовыми сдвигами / Сборник научных трудов НГТУ, 2014
Функциональные возможности - восстановление фазы по трём интерференционным картинам со случайными фазовыми сдвигами.
Особенности программы:
- Одновременно можно использовать только три интерференционные картины.
- Формат входных файлов - bmp(24 бит).
- Формат выходных файлов: bmp(24 бит), текстовый файл.
- Минимальный размер изображений 16x16 пикселей.
- Максимальный размер изображений 4096x4096 пикселей.
Инструментальные средства создания - Microsoft Visual Studio 2012, С++, NVIDIA CUDA 5.5
Работа с программой - в приложенном архиве располагается программа для OC Windows в виде исполняемого файла (папка redist) и в виде исходного кода (папка src). Для запуска программы необходимо запустить файл Phazes_on_CUDA.exe. В папке redist также можно найти руководство по работе с программой (Руководство.txt).
Общие:
1) OC Windows XP и выше
2) Видеокарта с поддержкой NVIDIA CUDA(Compute Capability не ниже версии 2.0)
Для запуска исполняемого файла:
1) Visual C++ Redistributable for Visual Studio 2012 (http://www.microsoft.com/en-us/download/details.aspx?id=30679)
Для компиляции исходного кода:
1) Microsoft Visual Studio 2012
2) NVIDIA CUDA 5.5
ClusterGenerator3D. Подсчет упорядоченных кластеров в 3D-пространстве
Назначение: Программа предназначена для определения количества упорядоченных кластеров, генерируемых случайным образом в 3D-пространстве.
Область применения: Программа может быть использована в области физики и материаловедения.
Используемый алгоритм: Реализованный в программе алгоритм заключается в подсчете кластеров, сгенерированных случайным образом. Кластеры реализованы в виде трехмерных цепочек шаров.
Алгоритм разработан автором и заключается в следующем:
1. В слое сгенерированных шаров выбирается первая цепочка и в ней производится поиск отдельных кластеров. Каждому новому обнаруженному кластеру присваивается свой порядковый номер от 1до N. Данные о нахождении какого-либо шара в кластере заносятся в массив.
2. С учетом первой (базисной) цепочки производится поиск в следующих цепочках. Если обнаруживается связь с уже обнаруженными кластерами, шару присваивается порядковый номер соответсвующего кластера, иначе шар является началом нового кластера и ему присваивается следующий порядковый номер.
3. Так как сгенерированные объекты могут представлять собой сложную структуру, поиск и проверка проводятся ещё несколько раз в зависимости от размеров структуры.
Функциональные возможности: С помощью данной программы можно определять количество упорядоченных кластеров, осуществлять обзор в режиме 3D, получать данные о свойствах генерируемых кластеров.
Инструментальные средства создания: Среда программирования Delphi 7.0 Lite
Поддерживаемые ОС: Windows XP/Vista/7/8
Процессор с тактовой частотой 800 МГц и выше
Разрешение экрана: не менее 1024х768 пикселей
Тренажер для контроля процесса построения обратной матрицы
Назначение - контроль построения обратной матрицы (выбор структуры элемента, последовательное вычисление алгебраических дополнений и определителя исходной матрицы, арифметические преобразования полученных элементов обратной матрицы).
Область применения - в учебных заведениях для выработки навыков или контроля приобретенных навыков у студентов при построении обратной матрицы.
Используемый алгоритм - генерация исходной матрицы и всех эталонных решений при получении обратной матрицы с последующим сравнением вводимых цифр и линейным поиском нужных комбинаций в эталонных решениях. Выбор структуры элементов производится путем обработки события, связанного со щелчком мыши, а ввод элементов происходит при обработке события, связанного с нажатием клавиш. Каждый щелчок кнопки мыши и нажатие клавиши обрабатываются контролирующими блоками с выводом информации о текущих ошибках, если они совершаются. Описание подобных программ приведено в статье [1].
1. Попов А.А., Бакланова Н.Б., Таныгина Т.А., Яньшина А.А. Интерактивные иллюстрации для задач линейной алгебры. "Применение информационно-коммуникационных в образовании(ИТО - Марий Эл - 2014): Материалы XI Всесоюзной научно-практической конференции. - С.131-138.
Функциональные возможности - программа может генерировать различные квадратные матрицы 2, 3 и 4 порядка, образовывать для них эталонные решения и подготавливать режим ввода символов с контролем каждого введенного символа. Ориентировочное время решения задачи составляет 1, 4 и 36 минут (соответственно для матриц 2, 3 и 4 порядка). Система комментариев в программе исключает неоднозначность при выполнении текущих действий.
Инструментальные средства создания - программа написана на языке Java с использованием среды Eclipse.
Во вложении запакованный файл ObrMatrTren.rar содержит 3 файла: ObrMatrTren.bat запускает программу ObrMatrTren.class на выполнение. При завершении программы ObrMatrTren.class автоматически используется класс WindowDestroyer.class для разрушения окна. В текстовом файле Trenazher.doc собрана текстовая и графическая информации о решении одного из примеров.
На компьютере должна быть установлена виртуальная Java машина, соответствующая используемой версии операционной системы Microsoft Windows (не ниже Microsoft Windows XP).
Использование алгоритма кластеризации для выделения контуров на изображениях
Назначение Программа предназначена для выделения контуров на цифровых изображениях.
Область применения Выделение контуров на цифровых изображениях применяется в процессе решения задач, связанных с анализом графических объектов: обработка спутниковых фотографий поверхности земли, обработка снимков биологических объектов под микроскопом, обработка медицинских данных, локализация текста на изображениях.
Используемый алгоритм Границы на изображении – это кривые, ограничивающие односвязные области одного цвета. Алгоритм ищет границы в два этапа. На первом этапе на изображении выделяются односвязные области одного цвета. На втором этапе ищутся кривые, ограничивающие данные области. Набор пикселей исходного изображения преобразуется в множество точек векторного пространства RGBXY (три цветовые координаты и две пространственные). Цветовые координаты каждой точки нормализуются.
Построенному множеству точек сопоставляется полносвязный граф. Длина ребра равна Евклидовому расстоянию между точками в пятимерном пространстве RGBXY. Для выделения односвязных областей одного цвета на изображении выполняется кластеризация построенного графа. Для кластеризации графа используем алгоритм, основанный на построении минимального остовного дерева (для его построения используется жадный алгоритм). При кластеризации минимальное остовное дерево разбивается на поддеревья. Разбиение производится отбрасыванием рёбер, превышающих некоторую длину на определённом шаге алгоритма. Для этого удаляются рёбра больше некоторого порога t = r_coefficient^iter * MAX_DISTANCE, где r_coefficient принадлежит (0, 1), MAX_DISTANCE – максимальное расстояние между двумя точками, iter – номер итерации. После удаления рёбер с весом, превышающим t, дерево разбивается на поддеревья, представляющие собой односвязные области на изображении.
В алгоритме также выполняется проверка, что размер полученных кластеров после разбиения превышает некоторый порог minimum_cluster_size; если размер кластера меньше данного порога, ребро, удаление которого привело к такому разбиению, не удаляется. Таким образом, на каждой новой итерации алгоритм производит более глубокую кластеризацию. Процесс кластеризации останавливается при t < percent * MAX_DISTANCE.
После проведения кластеризации для каждого кластера определяется его граница толщиной в один пиксель путём проверки количества соседей, входящих в данный кластер для каждого пикселя из этого кластера. Регулируя глубину кластеризации, можно управлять уровнем детализации выделяемых контуров.
Алгоритм разработан Кутлуниным П.Е. и Белимом С.В.. Подробное описание алгоритма можно найти в статье [1].
[1] Белим С.В., Кутлунин П.Е. Выделение контуров на изображениях с помощью алгоритма кластеризации // Компьютерная оптика. - 2015. Т. 39, № 4. - С. 119-124].
На вход программе подаётся 5 обязательных параметров:
1) file_name - путь к изображению, которое необходимо разбить на односвязные области;
2) r_coefficient - коээфициент уменьшения расстояния между рёбрами. Рёбра, превышающие значение r_coefficient * MAX_DISTANCE на очередной итерации, удаляются из дерева, тем самым распадаясь на поддеревья, представляющие собой односвязные области на исходном изображении. MAX_DISTANCE - максимальное расстояние между двумя рёбрами в исходном остовном дереве;
3) percent - процент от MAX_DISTANCE, при достижении значения которого алгоритм останавливает свою работу;
4) minimum_cluster_size - ограничение на минимальное количество пикселей в односвязной области;
5) color_intervals - количество цветовых интервалов, используемое для определения наиболее популярного для исходного изображения интервала и выбора первоначальной точки для построения дерева из этого цветового интервала.
После запуска программы в директории расположения программы будет создан файл с результатом работы программы с названием %original_name%_bounds.bmp, где original_name – название исходного файла file_name без расширения.
Результатом работы программы является изображение с выделенными границами областей (белый фон и чёрные границы).
Инструментальные средства создания программа написана на языке Java. Для написания использовались стандартные библиотеки классов JDK, в том числе классы из пакетов java.awt и javax.imageio для работы с изображениями.
Вложение прикреплён архив иboundsearchresults.zip, в котором представлены результаты работы программы для искусственных и фотографических изображений (всего 3 изображения). Программа запускалась со следующими параметрами: r_coefficient=0,8; percent=10; minimum_cluster_size=30; color_intervals=16.
установленная JRE версии не ниже 1.6
ОП: 256 Мб
ОС: любая, поддерживающая JVM.
Программа решения задач о покрытии множеств
Назначение - Решение задач о покрытии множеств
Используемый алгоритм - метод ветвей и границ с определениеи нижних, верхних границ на основе приближенного решения двойственных задач с помощью субградиентного метода. Для сокращения размерности по исходным и двойственным переменным используются логические процедуры. Логическое тестирование осуществляется в каждом узле дерева ветвей и границ. В процедуре ветвления в качестве входных данных используется вектор двойственных оценок, полученный на предшествующем уровне. Для ветвления в начале выбирается строка, соответсвующая максимальной компоненте вектора двойстенных оценок. Столбцы в выбранной строке упорядычиваются по возрастанию их приведенной стоймости. Для просмотра индексов по столбцам и строкам используются разреженные строчный и столбцовый форматы. При этом создаются только массивы индексов, а для элементов матрицы нет необходимости отводить память [1].
[1] Забиняко Г.И. Реализация алгоритмов решения задачи о покрытии множеств и анализ их эффективности // Вычислительные технологии -2007,Т.12,№6, с.50-58.
Разработаны варианты программ в однопроцессорном и многопроцессорном режимах.
Функциональные возможности - реально с обоснованием оптимальности решаются задачи с числом строк до 500 и столбцов до 5000.
Инструментальные средства создания - фортран, MPI
для использования в однопроцессорном режиме достаточно наличия компилятора фортрана,
для использоания в параллельном режиме необходима некоторая версия MPI.
Программный комплекс построения целочисленных моделей календарного планирования проектов
Назначение Построение математических моделей календарного планирования для точного решения задач минимизации длительности цикла работ сетевых моделей с ограниченными нескладируемыми ресурсами.
Область применения Управление сложными системами: опытное производство, предприятия единичного производства, проектно-конструкторские организации, ремонтное производство, календарное планирование проектов.
Используемый алгоритм Программный комплекс формирует целочисленные линейные модели для решения задач построения расписаний операций по критерию минимизации общего времени выполнения комплексов работ, заданных сетевыми моделями.
В моделях формализованы условия соблюдения частичного порядка выполнения работ (операций) и не превышения потребления нескладируемых ресурсов над их наличием во всех временных интервалах. Модели строятся в двух вариантах. В первом варианте допустимы только непрерывные операции. Во втором - возможны перерывы в выполнении операций в целые моменты времени. Для обоих вариантов моделей целевой функцией является минимизация завершения конечных работ проектов. Построенные модели в виде таблиц в MPS-формате формируются в текстовых файлах.
В первом варианте с непрерывными операциями каждой работе сопоставляется булева переменная, равная единице при завершении работы в данный момент времени. Для второго варианта каждой операции сопоставляются булевы переменные, сумма которых равна продолжительности операции и каждая из которых равна единице при выполнении работы в данном интервале времени, и - нулю, если операция в данном интервале не выполняется. В остальном постановки задач совпадают.
В программном комплексе реализованы алгоритмы построения целочисленных линейных моделей, приведенные в статьях[1], [2].
[1] Ляхов О.А. Целочисленная линейная модель задачи календарного планирования проектов с перерывами работ. Азиатская школа-семинар "Проблемы оптимизации сложных систем ", республика Казахстан, Усть-Каменогорск, 2010 г.;
[2] Ляхов О.А. Целочисленные линейные модели сетевого планирования и управления. Азиатская школа-семинар "Проблемы оптимизации сложных систем", Новосибирск, 2011.
Функциональные возможности Формат исходных данных соответствует правилам формирования исходных данных в известной библиотеке тестовых примеров PSPLIB. Предусмотрены варианты моделей с возможностью перерывов выполнения операций в целочисленные моменты времени и с непрерывным выполнением работ. На входе осуществляется синтаксический контроль исходных данных. Выходные данные формируются в MPS-формате в виде, пригодном для применения известных пакетов программ целочисленного программирования. Комплекс программ позволяет строить целочисленные модели для всех примеров из библиотеки PSPLIB (от 30 до 120 операций в сетевой модели).
Инструментальные средства создания Операционная система WINDOWS, язык FORTRAN.
ЭВМ PC с оперативной памятью не менее 2 Gb и HDD не менее 120 Gb. Операционная система WINDOWS XP/7/8/.
Программа "Термик" построения объемных температурных полей по данным автоматизированных измерений
Область применения Построение объемных температурных полей в геоинженерии, геотехнике, геотермике и горном деле по данным термометрических сетей в криолитозоне. Знание температурного состояния пород и грунтов оснований инженерных сооружений в крилитозоне - гидроузлов, надшахтных сооружений подземных рудников, эксплуатируемых зданий, ТЭЦ возведенных на вечной мерзлоте - залог их безопасной эксплуатации. Область применения программы также определяется тем, что более что 60% территории РФ географически расположено в криолитозоне Земли.
Описание алгоритма Алгоритм представляет собой численную реализацию авторской схемы (далее "схема") в рамках классической системы автоматизированного управления с прямыми и обратными связями. Предназначен для обработки пространственно распределенных температурных данных "рассеянного" типа в методе смены стационарных состояний при решении геотеплофизических задач для медленнопротекающих процессов, повсеместно возникающих в геоинженерии (особенно в осваиваемых районах Севера и Арктического шельфа).
Общие элементы алгоритма и некоторые результаты работы программы приведены в статье [1].
[1] В.В. Неклюдов, С.А. Великин, А.В. Малышев, Контроль температурного состояния оснований рудников в криолитозоне средствами автоматизированного мониторинга, Криосфера Земли, 2014, №4.
Для обеспечения геокриологической безопасности при эксплуатации инженерных объектов в криолитозоне "схема" использует проверенные и надежные алгоритмы 2D или 3D интерполяции "рассеянных" данных. Исходные температурные данные разбиты на два блока:
- температурные параметры объемных квазистационарных тепловых источников объекта: шахтный ствол, совокупность объемных вентиляционных каналов, система замораживающих колонок и термосифонов;
- температуры измерительной скважинной сети: вертикальные термометрические скважины и горизонтальные скважины, а также единичные температурные датчики на входе и выходе замораживающей системы.
"Схема" обеспечивает чтение геометрии объекта и геометрии скважинных термометрических сетей, а также элементы строительных чертежей, в соответствии с которыми формируется объемная сетка с температурными данными. После 2D или 3D интерполяции (опционально), "схема" позволяет вывести полученный температурный параллелепипед в формате, пригодном для чтения другими (по желанию Заказчика) профессиональными графическими системами.
Исходная геометрия объекта для "схемы" формируется по строительным чертежам в известной программе "Surfer".
"Схема" позволяет:
- работать с БД многолетних (автоматизированных) наблюдений и строить как геокриологические температурные разрезы, так и геокриологические разрезы скоростей промерзания-оттаивания, причем как в 2D, так и 3D виде;
- численно оценивать некоторые теплофизические характеристики (коэффициент температуропроводности и др.) грунтов и пород фундамента объекта непосредственно в полевых условиях как решение коэффициентной задачи простейшего уравнения теплопереноса;
- строить объемные изотермические поверхности в объеме фундамента (подземного рудника), в т.ч. и в динамике, что позволяет оценить пространственное распределение областей фазовых переходов и выйти на построение термодинамических характеристик грунтов фундамента.
"Схема" предоставляет возможность интерактивной работы с построенным кубом температурного поля:
- одним кликом перемещаться между глубинными и вертикальными срезами.
- одним кликом задавать дополнительные точки на глубинном срезе с указанием новой температуры в ней и проведением перерасчета интерполяции на этом глубинном срезе.
- осуществлять коррекцию коротких скважин в интервале экстраполяции.
Применение авторской опции "экстраполяции" коротких скважин до глубин длинных скважин существенно расширяет возможности объемных построений в геотехнической индустрии. Возможно использование других возможностей по желанию Заказчика
"Схема" предоставляет опцию "online - мониторинга" на дисплее производственного компьютера (по имеющейся истории многолетних температурных измерений) динамики температур по всем термометрическим скважинам фундамента надшахтных высотных сооружений подземного рудника. Такая возможность позволяет оператору замораживающей станции напрямую визуально фиксировать появление трендов аномальных температур в текущей динамике и реагировать на нестандартные ситуации путем задания дополнительных параметров в контуре обратной связи в САУ «термометрическая система -резидентная программа – замораживающая система».
"Схема" реализована для версии «CPU–расчетов», однако может быть перенесена на случай «GPU-расчетов».
Функциональные возможности Типичный объем обрабатываемых данных составляет до 8 Гб ОП для крупнейших подземных рудников в криолитозоне РФ на один типовой фундамент подземного рудника.
Детальность температурных построений алгоритмом программы "Термик" обеспечивается с детальностью до получения температурных градиентов на поперечном сечении сваи, с точностью до ее формы – круглая или квадратная. Точность собственно температурных построений обеспечивается точностью используемых температурных датчиков – как правило, до сотых градуса Цельсия. Погрешность также определяется аппаратурной составляющей. Такие возможности, предоставляемые алгоритмом программы «Термик», которые в настоящее время отсутствуют в других известных геотехнических системах, позволяют эксплуатационникам оценивать т.н. температурные деформационные напряжения на сваях и других элементах (тюбинги и проч.) в целях контроля их разрушения.
Инструментальные средства реализации алгоритма - семейство C++, в описываемой версии 64bit - программных сред программирования. Для пользователя поставляется в виде исполняемого файла.
32\64 Bit PC, ~8 Gb RAM, Pentium\AMD, Windows 7/8.
Быстрое вейвлет-преобразование в пространстве сплайновых вейвлетов на конечном отрезке
Область применения - анализ данных, численные методы.
Вейвлет-системы дают ряд преимуществ для широкого круга задач перед классическими ортогональными системами функций благодаря своим аппроксимационным свойствам и локализации во временной и частотной областях. Вейвлеты чрезвычайно перспективны для применения в задачах обработки сигналов, распознавания образов, сжатия информации.
Программа позволяет построить прямое и обратное вейвлет-преобразование на базе полиномиальных сплайнов. В программе реализованы следующие возможности:
- построение вейвлет-базисов в пространстве полиномиальных сплайнов;
- получение графиков и матрицы значений центральных и граничных вейвлет-функций;
- получение коэффициентов вейвлет-преобразования по набору входных данных и обратно;
- определение начальных параметров преобразования - отрезка и степни спалйна;
- сохранение полученных данных в виде отчета;
Алгоритм реализован для полиномиальных сплайнов степени m={2,3,4}.
Объем входных-выходных данных для обратного вейвлет-преобразования:
| Степень сплайна | Кол-во входных параметров - коэффициентов преобразования | Кол-во выходных параметров - значений функции на сетке |
| 2 | 9 | 8 |
| 3 | 18 | 16 |
| 4 | 35 | 32 |
Входным параметром для прямого вейвлет-преобразования является функция, выходными данными является набор коэффициентов преобразования (соответствует второму столбцу таблицы).
В приложениях важно уметь решать две следующие задачи:
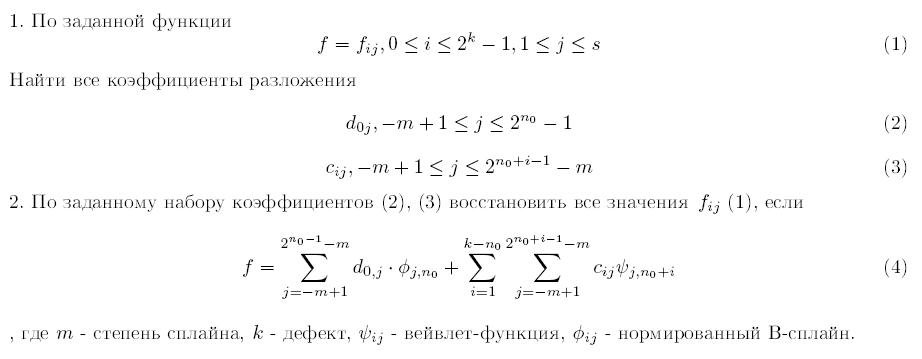
Решение первой задачи называется прямым вейвлет-преобразованием, решение второй задачи - обратным вейвлет-преобразованием. Поскольку носители построенных вейвлет-функций содержат конечное, не зависящее от дефекта, число частичных отрезков, то они очень хорошо локализованы во временной области. Т.к. они являются линейными комбинациями фиксированного числа B-сплайнов, то они хорошо локализованы и в частотной области. Поэтому коэффициенты разложения по ним непериодического сигнала несут как информацию о его поведении на коротком отрезке времени, так и о его "мгновенном спектре".
Используемые материалы - работы заведующего кафедры Высшей математики Поволжского государстенного университета телекоммуникаций и информатики д.ф.-м.н. Блатова Игоря Анатольевича, в частности алгоритм вейвлет-преобразования на основе полиномиальных сплайнов, используемый в основе программы.
Инструментальные средства создания - C++ Builder 6.
Во вложении два главных файла:
- FWTSplain.pdf - описание программы;
- FWTSplain.zip - архив с исходным кодом программы.
Литература:
- Блатов И.А. Полуортогональные сплайновые вейвлеты и метод Галеркина численного моделирования тонкопроволочных антенн / И.А.Блатов, Н.В.Рогова // Журнал вычислительной математики и математической физики. Самара, том 53, №5 : 2013. 727-736 с.
- Блатов И.А. Псевдоразреженные матрицы и прикладной вейвлет-анализ, Сборник научных трудов sworld по материалам международной научно-практической конференции, 2012, 84–86 с.
ОС - Windows XP и выше;
Свободная память 20 Mb;
RAM 30 Mb.
Гибридный локальный поиск для задачи маршрутизации транспортных средств с распределенными поставками
Область применения - логистика, транспортные задачи.
Назначение - нахождение приближенных решений для задачи маршрутизации транспортных средств с разделеннымы поставками (Split Delivery Vehicle Routing Problem)
Постановка задачи. В задаче маршрутизации транспортных средств неограниченный автопарк одинаковых транспортных средств расположен на складе. Каждое транспортное средство имеет фиксированную вместимость. Маршрут транспортного средства должен начинаться и заканчиваться на складе. Есть множество клиентов, рассположенных на плоскости. Каждый клиент имеет заданный запрос на доставку. Задача заключается в поиске набора маршрутов транспортных средств с минимальной суммарной длиной маршрутов при условии, что все клиенты будут обслужены. В задаче маршрутизации транспортных средств с разделенным обслуживанием (SDVRP) каждый клиент может быть посещен несколько раз, и поставки по его запросу могут быть разделены между транспортными средствами.
Используемый алгоритм - гибридная метаэвристика, сочетающая в себе локальный спуск по чередующимся окрестностям и стохастический поиск с запретами. Подробно описан в прилагаемом файле.
Функциональные возможности - программа позволяет находить приближенные решения с малой погрешностью для задачи маршрутизации транспортных средств с разделенными поставками. При размерности до 288 клиентов алгоритм находит решение с погрешностью не более 3%. Ограничение на размерность задачи отсутствует, но при большей размерности требуется больше временных ресурсов.
Инструментальные средства создания - Java 6.0, Eclipse IDE.
Исходный код находится в прикрепленном архиве. Для запуска работы необходимо установить Eclipse или любую другую IDE для работы с Java. Главный класс находится в пакете "tests". Один из них для запуска одного из примеров, другой для вычисления всего множества примеров. Также в приложении есть рисунок, в котором приведен результат работы программы для размерности в 64 клиента. Красным выделены клиенты с разделенной поставкой.
Алгоритм опубликован в статье: Alexey Khmelev, Yury Kochetov. A Hybrid Local Search for the Split Delivery Vehicle Routing Problem. International Journal Of Artificial Intelligence 2015, Vol 13, 1
Java 6.0
- « первая
- ‹ предыдущая
- …
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- …
- следующая ›
- последняя »
