Расчет быстрого преобразования Фурье на графическом процессоре с использованием технологии Nvidia CUDA
Назначение: Расчет прямого и обратного преобразования Фурье.
Область применения: Цифровая голография, оптическая физика.
Используемый алгоритм: Алгоритм преобразования Фурье методом Кули-Тьюки (Cooley-Tukey). Алгоритм Кули-Тьюки позволяет значительно сократить количество операций для двумерного дискретного преобразования Фурье [1]. Распараллеливание происходит на платформе CUDA, в которой выполняется элементарная операция Алгоритма Кули-Тьюки, так называемая «бабочка» над элементами массива.
1. Блейхут Р. Быстрые алгоритмы цифровой обработки сигналов: Пер. с англ.—М.: Мир, 1989.—448 с.
Используемые сокращения: FFT - Fast Fourier Transform (быстрое преобразование Фурье), iFFT - Inverse Fast Fourier Transform (обратное быстрое преобразование Фурье)
Программа выполняет следующие функции:
- Загрузка изображения формата jpg.
- Преобразование изображение в массив комплексных чисел.
- Расчет прямого преобразования Фурье методом Кули-Тьюки (по нажатию на кнопку FFT)
- Расчет обратного преобразования Фурье методом Кули-Тьюки (по нажатию на кнопку iFFT)
Работа с программой: в приложенном архиве располагается программа для OC Windows в виде исполняемого файла (папка redist) и в виде исходного кода (папка src). Для запуска программы необходимо запустить файл GPU_FFT.exe (для примера приложено изображение 512.jpg). На вход подается изображение, из него формируется комплексный массив данных. Данный массив подается на графическую видеокарту, в которой производится расчет преобразования Фурье.
Функциональные возможности:
- Расчет прямого и обратного преобразования Фурье методом Кули – Тьюки.
- Запись получившихся преобразований в файл. Вывод информации о видеокарте.
- Обработка изображений не более чем 8096х8096 пикселей.
Инструментальные средства создания: Microsoft Visual Studio 2013, CUDA Toolkit 7.5.
Общие:
1) OC Windows 7 и выше
2) Оперативная память не менее 2ГБ
Для запуска исполняемого файла:
1) Visual C++ Redistributable for Visual Studio 2013 (https://www.microsoft.com/ru-RU/download/details.aspx?id=40784)
2) CUDA Toolkit 7.5 (https://developer.nvidia.com/cuda-downloads)
Для компиляции исходного кода:
1) Microsoft Visual Studio 2013
2) CUDA Toolkit 7.5
Численный алгоритм решения обратной задачи для системы дифференциальных уравнений
Назначение - Программа предназначена для численного решения обратной задачи для линейных систем обыкновенных дифференциальных уравнений с правыми частями.
Область применения - Процессы, характеризующиеся системами линейных дифференциальных уравнений (например, фармакокинетика).
Используемый алгоритм - В работе рассмотрена вариационная постановка обратной задачи для линейной системы дифференциальных уравнений с правыми частями [1]. С помощью введения сопряженной задачи в явном виде была получена матрица градиента целевого функционала (подробное описание алгоритма, вид градиента и сопряженной задачи в файле "Инструкция по работе с программой"). Задача оптимизации решается методом итераций Ландвебера. В программе предусмотрены следующие функции:
1. Задание точности решения.
2. Задание временного интервала.
3. Задание параметра метода итераций Ландвебера.
4. Возможность фиксировать параметры в системе дифференциальных уравнений.
5. Возможность ограничения определяемых параметров интервалом допустимых значений.
6. Задание правых частей системы в виде экспонент.
Инструментальные средства создания - Программа написана на языке программирования C++ в среде разработки Visual Studio 13.
[1] А.И. Ильин, С.И. Кабанихин, Д.А. Воронов, Универсальный подход к решению обратной задачи фармакокинетики в случае произвольного количества камер // Сибирские электронные математические известия. «Труды V международной молодежной школы-конференции "Теория и численные методы решения обратных и некорректных задач". 2014. Т. 11. С. С41-С49
Алгоритм разработан в рамках гранта РФФИ № 16-31-00382.
Компьютер на базе Windows XP (и выше) с оперативной памятью 512 МБ (и больше).
Геоинформационная система "Банк данных природных катастроф Земли" (GIS-ENDDB)
|
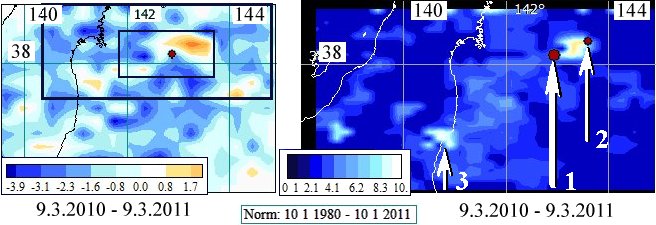
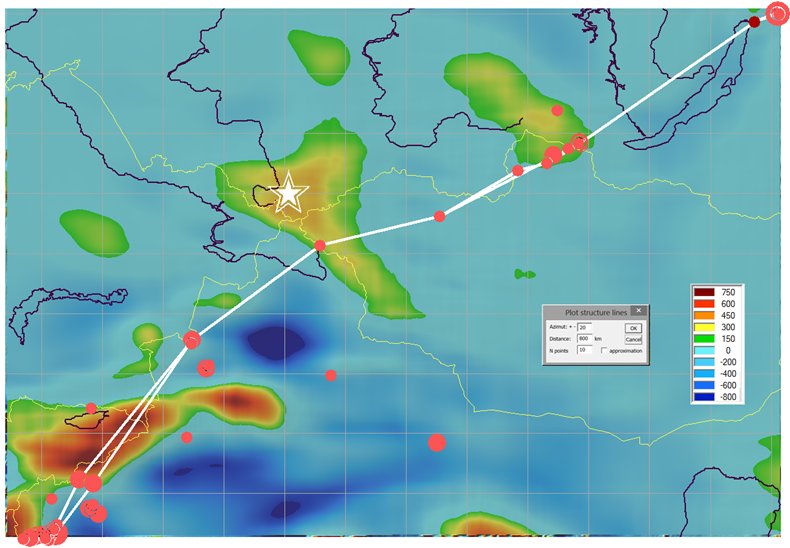
Назначение - для исследования исторических природных катастроф (землетрясений и космических ударов) и выявления структур сейсмичности и метеоритных кольцевых структур математическими и геоинформационными средствами по данным пользовательских каталогов. Область применения - геодинамика, геотектоника. Используемые алгоритмы - расчет характеристик сейсмического режима, построение линеаментов сейсмичности, построение карт осредненного значения характеристик (на рисунке приведен расчет сейсмических затиший перед Великим Восточным Японским землетрясением и их градиента). Подробное описание алгоритмов в [1,2]. 1. Михеева А.В., Дядьков П.Г., Марчук А.Г. Геоинформационная система GIS-EEDB и методы пространственно-временного анализа сейсмологических данных // Геоинформатика, 2013. – № 2. – С. 58-65. 2. Mikheeva A.V., Marchuk An.G., Dyadkov P.G. Geoinformation Systems for Studying Seismicity and Impact Cratering using Remote Sensing Data // In Book: “Geographic Information Systems (GIS): Techniques, Applications and Technologies”. - Nantes University, France: Nova Science Publishers, 2014. – 65 p.
Функциональные возможности- ограничений на объем пользовательских данных нет, максимальный размер файла растровой информации в настоящий момент составляет 18 Гб, наиболее полный каталог - 2722946 записей. Некоторые функции: - отрисовка фоновых карт (рельефа, гравики, теплового потока), - вывод данных импактного и сейсмологического каталогов (координаты, время, диаметр/магнитуда и прочие характеристики), задание детальности ЦМР (от 30'' до 1”), - инструмент построения разрезов с отображением рельефа фонового поля и сейсмологических данных, - функция построения линеаментов (на рисунке представлен результат работы алгоритма - линеамент событий за неделю до Чуйского землетрясения на фоне карты аномалий силы тяжести)
Инструментальные средства создания - Visual Studio, FoxPro, ActiveBar. Алгоритмы опубликованы в журнале "Геоинформатика" и "Bulletin NCC. Series: Mathemaical Modeling in Geophysics":
|
Windows 98 и выше, 32 и 64-разрядные версии ОС, от 6 Гб жесткого диска.
Принятие решения о надёжности (ненадёжности) сети с ограничением на диаметр по отношению к заданному порогу
Назначение – позволяет устанавливать, является ли сеть достаточно надёжной(ненадёжной) по отношению к заранее заданному порогу надежности для сети с ограничением на диаметр.
Область применения - анализ надёжности сетей различного назначения.
Рассматриваются сети, в которых отказам подвержены только каналы связи. Под надёжностью понимается вероятность того, что все выделенные узлы связаны между собой с помощью исправных каналов связи путями оганиченной длины. Точный расчет надёжности сети является NP-трудной задачей. Однако при анализе сети иногда достаточно знать, превосходит ли надёжность исследуемой сети величину заданного порога. Используя метод Cancela и Petingi [2], можно организовать итерационный процесс уточнения верхней и нижней границы надёжности сети с ограничением на диаметр и остановить его при достижении одной из границ значения заданного порога. Подобный подход для сетей без ограничения на диаметр был предложен в [1]. Программа позволяет устанавливать, является ли сеть достаточно надёжной по отношению к заданному порогу надежности, а также можно выбрать максимальное время работы, через которое программа остановится, показав верхнюю и нижнюю границы надёжности сети.
[1] Won J.-M., Karray F. Cumulative Update of All-Terminal Reliability for Faster Feasibility Decision // IEEE Trans. On Reliability. September 2010. Vol 59, no 3. P. 551-562.
[2] Hector Cancela and Louis Petingi. Diameter constrained network reliability: exact evaluation by factorization and bounds. In ICIL’2001 (International Conference on Industrial Logistics), pages 359– 366, 2001.
Входные данные программы – структура сети в виде графа, значения надёжности каналов связи (т.е. вероятности их присутствия), значение порога (число от 0 до 1) (можно отключить), ограничение на время расчёта в секундах (можно отключить).
Выходные данные программы – ответ о достаточной надёжности/ненадёжности сети. Если расчёт не был окончен за отведённое время, выводятся полученные к данному моменту значения границ надёжности.
Программа работает с графом, представленным полным файлом предшественников (списки KAO,FO), а также списком терминалов. Вводить списки представления графов и редактировать их можно в соответствующих окнах программы. Информация в файле располагается следующим образом: первая строка и вторая строка – списки KAO и FO соответственно, в третьей строке располагается список терминалов сети (Ki=1, в случае, если i-я вершина сети является терминалом, и 0 иначе). Четвёртая строка – значение надёжности каждого ребра, пятая – значение диаметра сети.
Алгоритм разработан в рамках гранта РФФИ № 14-07-31069.
Функциональные возможности – анализ надёжности сетей с количеством элементов в несколько сотен.
Инструментальные средства создания – Microsoft Visual Studio 2012.
OS: Windows
Необходима та же версия .Net framework’a, на которой была собрана программа: V4.5.
Иначе программу можно собрать из исходного кода
Расчёт надёжности сети с ограничением на диаметр с использованием предварительной редукции и выбором оптимального ребра в процессе факторизации
Назначение – позволяет вычислять точное значение надёжности K-терминальной сети с ограничением на диаметр.
Область применения - анализ надёжности сетей различного назначения.
Одним из важных показателей сетевой надежности является вероятность связности заданного подмножества узлов. Однако существует также множество случаев, когда обычной связности терминалов недостаточно и необходимо, чтобы длина связующего пути не превышала заранее заданного числа D. Как и задача расчёта надёжности сети, задача расчёта надёжности сети с ограничением на диаметр NP-трудна [1]. В данной программе используется метод Cancela и Petingi вычисления точного значения K-терминальной надёжности сети с ограничением на диаметр, а также методы ускорения работы программы, предложенные в [2]: предварительные сортировка рёбер, а также редукции рёбер.
[1] Cancela H., Petingi L. Reliability of communication networks with delay constraints: computational complexity and comlete topologies // Int. J. of Mathematics and Mathematical Sciences. 2004. V. 29. P. 1551-1562.
[2] D. Migov and S. Nesterov. Methods of Speeding up of Diameter Constrained Network Reliability Calculation // Springer Lecture Notes in Computer Science (in ICCSA 2015). Volume 9156, 2015, pp. 121-133.
Входные данные программы – структура сети в виде графа, значения надёжности каналов связи (т.е. вероятности их присутствия).
Выходные данные программы – значение надёжности сети.
Программа работает с графом, представленным полным файлом предшественников (списки KAO,FO), а также списком терминалов. Вводить списки представления графов и редактировать их можно в соответствующих окнах программы. Информация в файле располагается следующим образом: первая строка и вторая строка – списки KAO и FO соответственно, в третьей строке располагается список терминалов сети (Ki=1, в случае, если i-я вершина сети является терминалом, и 0 иначе). Четвёртая строка – значение надёжности каждого ребра, пятая – значение диаметра сети.
Алгоритм разработан в рамках гранта РФФИ № 14-07-31069.
Функциональные возможности – расчёт надёжности сетей с количеством элементов около сотни.
Инструментальные средства создания – Microsoft Visual Studio 2012.
OS: Windows
Необходима та же версия .Net framework’a, на которой была собрана программа: V4.5. Иначе программу можно собрать из исходного кода
Оптимизация структуры сети по критерию надёжности с использованием кумулятивных оценок границ надёжности
Назначение - структурная оптимизация сетей различного назначения с целью повышения надёжности.
Область применения - моделирование и проектирование сетей различного назначения.
Используемый алгоритм - генетический алгоритм с использованием кумулятивных оценок верхней и нижней границ надёжности. Программа позволяет для заданного числа узлов и каналов связи сети находить структуру сети, оптимальную или близкую к оптимальной по критерию надёжности. Под надёжностью понимается вероятность связности сети. Узлы сети предполагаются абсолютно надёжными, т.е. надёжность узлов предполагается на порядки выше надёжности каналов связи. Для каждого канала связи задаются значения надёжности и стоимости прокладки. Поиск ведётся в условиях наперёд заданных ограничений на общую стоимость прокладки каналов связи и диаметр сети. Подход с использованием кумулятивных оценок позволяет быстрее принимать решение о пригодности (непригодности) получаемых в процессе работы алгоритма вариантов топологии сети.
Алгоритм опубликован в следующих работах:
[1] K. Nechunaeva, D. Migov. Speeding Up of Genetic Algorithm for Network Topology Optimization with Use of Cumulative Updating of Network Reliability // Proc. 9th Int. Conference on Ubiquitous Information Management and Communication (ACM IMCOM 2015), Bali, Indonesia, 2015. ACM New York, USA, 2015. ISBN 978-1-4503-3377-1. Article No. 42. (Indexed by Scopus)
[2] Д.А. Мигов, К.А. Нечунаева, А. С. Родионов Генетический алгоритм структурной оптимизации сетей с применением подхода кумулятивного уточнения границ надёжности. Вестник СибГУТИ, 2015, № 4. В печати.
Входные данные программы: количество узлов и каналов связи сети, значения надёжности для всех каналов связи (числа от 0 до 1), значения стоимости прокладки для всех каналов связи, параметры генетического алгоритма (размер популяции, кол-во поколений, размер турнира, вероятность мутации), ограничения на общую стоимость прокладки каналов связи, максимальное значение диаметра графа.
Функциональные возможности - структурная оптимизация сетей с количеством каналов до 100.
Инструментальные средства создания - Delphi.
Алгоритм разработан в рамках гранта РФФИ № 14-07-31069.
CPU: 1000 MHz
OS: Windows
Тренажер с посимвольным контролем процесса решения линейного дифференциального уравнения методом Лагранжа
Назначение - для ввода всех промежуточных и окончательных формул решения линейного дифференциального уравнения первого порядка методом Лагранжа с контролем каждого введенного символа.
Область применения - лекции и практические занятия по дифференциальным уравнениям.
Используемый алгоритм - формирование эталонного решения линейного дифференциального уравнения первого порядка методом Лагранжа в виде массива строк языка Java с последующим представлением их массивами символов с информацией о месте расположения каждого символа в окне программы. В программе обрабатывается каждое нажатие клавиши, во время которого для текущего символа находится или не находится соответствующий символ в эталонном решении. В одном случае символ добавляется к решению, в другом - выводится информация об ошибке. Более подробно алгоритм изложен в статье [1].
1. Попов А.А. Методика программирования на языке Java тренажеров по математике с посимвольным контролем аналитических преобразований. Программная инженерия. 2012. №8, с.38-43.
Функциональные возможности - программа может генерировать различные линейные дифференциальные уравнения с использованием не менее 100 шаблонов уравнений и обрабатывать каждый введенный символ при решении уравнения методом Лагранжа с генерацией ошибок.
Инструментальные средства создания - программа написана на языке Java с использованием среды Eclipse.
Во вложении файл TrainLagrange.zip содежит 7 файлов: файл с расширением .bat необходим для загрузки TrainLagrange.class, который в процессе выполнения использует остальные файлы.
В файле с расширением .doc показана работа с тренажером на конкретном примере.
Операционная система не ниже Microsoft Windows XP Professional и соответствующая операционной системе виртуальная машина Java.
Интерактивная иллюстрация процесса решения линейного дифференциального уравнения методом Лагранжа
Назначение - для иллюстрации процесса решения линейного дифференциального уравнения первого порядка методом Лагранжа с посимвольным выводом решения.
Область применения - лекции и практические занятия по дифференциальным уравнениям.
Используемый алгоритм - из массива сложных функций, имеющих различные аргументы, составляется линейное дифференциальное уравнение первого порядка и записывается его решение методом Лагранжа в виде массива строк языка Java. Каждая строка имеет управляющие символы, определяющие варианты размещения фрагментов строк в ее графическом представлении. Счетчик выводимых графических символов изменяется в методе run интерфейса Runnable после временной задержки. Более подробно алгоритм изложен в статье [1].
1. Попов А.А. Методика программирования на языке Java тренажеров по математике с посимвольным контролем аналитических преобразований. Программная инженерия. 2012. №8, с.38-43.
Функциональные возможности - программа управляется 4 клавишами, посредством которых запускается или останавливается поток, а также уменьшается или увеличивается время задержки перед выводом текущего символа. Программа является электронным эквивалентом процесса написание символов на аудиторной доске.
Инструментальные средства создания - программа написана на языке Java с использованием среды Eclipse.
Во вложении файл IllustrLagrange.zip содержит 7 файлов: файл с расширением .bat необходим для загрузки IllustrLagrange.class, который в процессе выполнения использует остальные файлы.
В файле с расширением .doc приведено решение одной из задач.
Операционная система не ниже Microsoft Windows XP Professional и соответствующая операционной системе виртуальная Java машина.
Выбор метода аппроксимации
Назначение:
- расчет и нахождение аппроксимирующих функций, с последующим построением аппроксимаций различными методами;
- расчет относительной ошибки аппроксимации как на всем заданном интервале функции, так и в отдельных ее точках;
- расчет значений аппроксимирующих функций на заданном интервале.
Область применения: Изучение новых объектов (технических) исследований при помощи методов аппроксимации, например, при исследовании вольт-амперной характеристики (ВАХ) электрорадиоизделий; исследование радиосигналов, т.е. амплитудно-частотных характеристик (АЧХ); при групповой архивации (сжатии) файлов - определение среднего соотношения эффективности сжатия информации.
Используемый алгоритм: метод наименьших квадратов разных функций и интерполяция (полиномы Ньютона и Лагранжа).
Блок-схема алгоритма приведена во вложении.
Для работы программы вводятся входные данные (значения X, Y), указываются шаг уплотнения и интервал (в каких пределах рассматривать функцию и производить расчет). По нажатию на кнопку "Расчет" производятся: расчет n методов аппроксимации, расчет погрешности с последующим внесением результатов в соответствующие таблицы и с построением графиков. По минимальному значению расчитанной погрешности определяется оптимальный метод аппроксимации.
Функциональные возможности: Программа позволяет представлять данные расчетов как в графической форме, так и в табличной. Возможность копирования результатов: расчеты в Microsoft Excel (таблицы); график в буфер обмена, а также печать на принтер. Входные данные: ручной ввод или текстовый файл. Объем обрабатываемых данных: до 5000 точек (X, Y), свыше 5000 - требуются более высокие параметры аппаратных средств ПК.
Инструментальные средства создания: среда разработки Borland Delphi 7.
Скриншоты:
1. Расчет значений аппроксимирующей функции и сама функция (модель);
2. Расчет погрешности (относительной ошибки аппроксимации) на всём интервале значений;
3. Расчет погрешности (относительной ошибки аппроксимации) в каждой точке для каждого метода аппроксимации;
4. Выбор метода аппроксимации на основе минимального значения расчитанной погрешности (в каждой точке);
5. Графическое представление расчитанной погрешности (для каждого метода аппроксимации);
6. Графики: входных данных (X,Y) и ее аппроксимации.
В качестве входных данных использовались экспериментальные значения ВАХ кремниего транзистора. В результате получили аппроксимирующую функцию.
Для эксплуатации необходимы следующие минимальные требования:
Процессор: Core 2 Duo частотой не ниже 1,5 ГГц;
ОЗУ: не менее 1 Гб;
ОС: Windows XP, Windows 7 (32 bit);
Свободное пространство на жестком диске не менее 50 Мб.
Видеокарта: 64 Мб.
Компьютерная модель движения финансовых потоков на фондовом рынке
Назначение - прогнозирование финансовых потоков
Область применения - валютные и финансовые рынки
Используемый алгоритм - алгоритм Бокса-Дженкинса с 14 параметрами. Нахождение параметров модели было сведено к решению двух взаимосвязанных задач квадратичного программирования. По разработанному алгоритму было создано программное обеспечение в среде MS Excel, обеспечивающее нахождения прогнозного значения отношения цен бивалютной пары евро-канадский доллар по 42 входным начальным данным.
Согласно теории Бокса-Дженкинса, прогнозное значение xt бивалютной пары в момент времени t определяется рекуррентным выражением:
xt = a1xt-1+...+ apxt-p+b1et-1+...bqet-q (1)
В выражении (1) приняты следующие обозначения:
- p, q – натуральные числа – число точек, участвующих в прогнозе;
- xt-p,...,xt-1 – последовательность значений в моменты времени с номерами t-p,..., t-1 соответственно;
- et-q,...,et-1 – случайные величины, имеющие нормальное распределение с нулевым математическим ожиданием и среднеквадратичным отклонением d;
- ai, bj – постоянные коэффициенты.
Для отыскания параметров ai, bj обычно используют метод перебора, суть которого заключается в «подгонке» параметров так, чтобы точки, получаемые из рекуррентного выражения (1), совпадали (или хотя бы были очень близки) с фактическими значениями. Данная методика дает хорошие результаты лишь для небольшого числа параметров (не более 3).
Научной новизной настоящего исследования является организация поиска параметров ai , bj посредством решения задачи квадратичного программирования.
Для простоты изложения далее считается, что p=q и число значений n временного ряда кратно p. Предположение n=kp (где k=1,2,…) не является критичным, т.к. его выполнение всегда можно обеспечить. Противоположный случай рассматривается аналогично, но получаемые выкладки будут более громоздкими и затруднят понимание идеи излагаемого метода.
Параметры a1, a2, …, ap трендовой составляющей определяются на основании выражения:
xt = a1xt-1+...+apxt-p (2)
Уравнению (2) можно сопоставить характеристическое уравнение
f(z)=1-a1z-...-apzp=0. (3)
В дальнейшем будут рассматриваться только стационарные процессы. Необходимым и достаточным условием стационарности процесса (2) является нахождение всех корней характеристического уравнения (3) вне единичного круга. Из этого условия следуют два неравенства
f(-1)f(1)>0,|ap|<1 (4)
Параметры a1, a2, …, ap, кроме условий (4), должны достаточно точно аппроксимировать фактические значения Таким образом, поиск коэффициентов a1, a2, …, ap трендовой части рекуррентного выражения (1) сведён к задаче квадратичного программирования с ограничениями (4).
Аналогичным образом можно определить параметры b1, b2, …, bp. Введя обозначение et=xt-a1xt-1-apxt-p, рекуррентное выражение (1) можно представить в виде:
et.=b1xt-1+...+bqxt-q (5)
Предполагая стационарность процесса (5) для поиска параметров b1, b2, …, bp, получается аналогичная задача квадратичного программирования.
Функциональные возможности - из таблицы валютных котировок в разработанное программное средство вводятся значения курса валют. Количество данных должно быть кратно 7 и не более 42. Проведя тестирование программного средства на большом количестве примеров, выяснилось, что кратность 7 вводимых данных обеспечивает достатчно качественный прогноз.
Инструментальные средства создания - табличный процессор MS Excel
Пакет MS Office 2003,2007, MS Excel 2003,2007
- « первая
- ‹ предыдущая
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- …
- следующая ›
- последняя »